Notowania
Waluty NBP
Kalkulatory

Wyobraźmy sobie, że chcemy ulokować w banku 1000 zł. Bank oferuje dwa rodzaje lokat: roczną o oprocentowaniu 15% i kwartalną o oprocentowaniu 14,25% w skali roku. Oprocentowanie pierwszej lokaty jest wyższe, jednak jeżeli będziemy odnawiać lokatę kwartalną przez rok, nie wypłacając odsetek, to na koniec roku otrzymamy w pierwszym przypadku 1150 zł, a w drugim 1150,30 zł, mimo, że oprocentowanie tej lokaty jest niższe. Mechanizm ten znany jest pod nazwą procentu składanego - wykorzystujemy po prostu fakt, że drugim kwartale odsetki naliczane są nie tylko od kapitału początkowego, ale także od odsetek zarobionych w kwartale pierwszym.
Kwotę, jaką otrzymamy przy likwidacji lokaty rocznej, można obliczyć za pomocą prostego wzoru:

kwota na zakończenie okresu lokaty = kwota wkładu *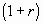

Przez r oznaczyliśmy stopę oprocentowania lokaty w skali roku.

Przykład
Przy założonej przez nas kwocie i oprocentowaniu obliczenie będzie wyglądać następująco:
kwota na zakończenie okresu lokaty =1000 zł * (1+0,15)= 1150 zl.

W przypadku lokaty kwartalnej, przedłużanej na okres roku obliczenia nie są dużo bardziej skomplikowane. Kwotę otrzymaną na koniec roku obliczymy przy pomocy wzoru:

kwota na zakończenie okresu lokaty = kwota wkładu *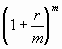

W tym wzorze r oznacza również stopę oprocentowania w skali roku, m jest to ilość podokresów w roku (w tym przypadku cztery kwartały).

Przykład
Przy założonej przez nas kwocie i oprocentowaniu obliczenie będzie wyglądać następująco:

kwota na zakończenie okresu lokaty =1000 zł * (1+(0,1425/4))⁴=1000 zł * 1,0.35625⁴=1150,3 zł

Jeżeli weźmiemy pod uwagę długi okres, zobaczymy, że niezbyt wielka różnica w stopach zwrotu może przełożyć się na bardzo duże różnice w końcowym stanie rachunku. Poniższa tabela pomoże Wam ocenić siłę procentu składanego. Zakładamy, że inwestujemy 10 000 zł i w okresie oszczędzania nie wypłacamy odsetek ani też nie dopłacamy żadnych kwot